KELAS 8 ( DARING 11 JANUARI 2021 )

 

• Teorema atau Dalil Phytagoras hanya berlaku pada segitiga siku-siku
•  dimana kuadrat sisi miring sama dengan jumlah kuadrat sisi yang lainnya

PAHAMILAH VIDEO DI BAWAH INI !

Contoh Soal dan Pembahasan Teorema Pythagoras

Sebuah tangga yang memiliki panjang 14 m bersandar dinding, jarak ujung tangga bagian atas ke lantai ialah 10 m. tentukan jarak kaki tangga ke dinding!

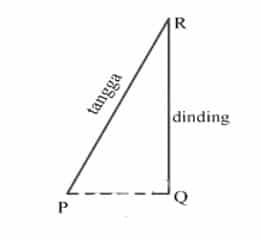
Penyelesaiannya:

Diketahui :

Tangga (PQ) = 14 m
Jarak tangga ujung tangga ke lantai ( QR) = 10m

Ditanya : Jarak kaki tangga ke dinding = PQ..?

Jawab :

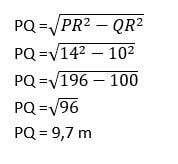
Jadi, jarak kaki tangga ke dinding ialah 9,7 m.

Tripel Pythagoras

Untuk menentukan salah satu sisi pada segitiga siku-siku dengan cepat dapat dilakukan dengan mudah dan tanpa menggunakan teorema Pythagoras. Caranya kamu dapat menggunakan tripel Pythagoras.

             

Berikut ini daftar tripel Pythagoras.

                

Pasangan tripel ini berlaku untuk kelipatannya.

Contoh

Buktikan bahwa 12, 5, 13 merupakan tripel Pythagoras.

Jawab:

Misalkan a = 12, b = 5, dan c = 13.

Berarti, a2 = 144, b2 = 25, dan c2 = 169.

Kamu dapat mengamati bahwa a2 + b2 = 144 + 25 = 169.

Jadi, c2 = a2 + b2 .

Ini berarti, 12, 5, 13 memenuhi teorema Pythagoras sehingga ketiga bilangan tersebut merupakan tripel Pythagoras.

Karakteristik Suatu Segitiga

Sebaai contoh, diketahui sebuah segitiga siku-siku dengan panjang sisi miringnya (sisi terpanjang) yaitu c. Serta panjang sisi-siki penyikunya yaitu a dan b, sehingga:

• Apabila c² < a²  + b², maka segitiga tersebut termasuk segitiga lancip;
• Apabila c² = a²  + b², maka segitiga tersebut termasuk segitiga siku-siku;
• Apabila c² > a²  + b², maka segitiga tersebut termasuk segitiga tumpul.

Untuk lebih jelasnya, perhatikan contoh soal di bawah ini:

Soal 

Suatu segitiga siku-siku ABC dengan siku-siku berada di B. Tentukan jenis segitiga tersebut jika telah diketahui panjang sisi AB = 8 cm, BC = 15 cm, dan AC = 20 cm!

Jawab:

Misalnya a merupakan sisi terpanjang dan b, c merupakan dua sisi lainnya, maka dapat kita ketahui jika:

• c = 20 cm
• b = 8 cm
• a = 15 cm.

c² = 20² = 400
a²  + b² = 8²  + 15² = 64 + 225 = 289

Sebab,

c² > a²  + b²
400 > 289

Sehingga, segitiga ABC termasuk ke dalam segitiga tumpul.

KERJAKAN : TUGAS INDIVIDU