DARING 1 SEPTEMBER 2021

MENENTUKAN NILAI LIMIT TRIGONOMETRI 

DENGAN METODE MENYEDERHANAKAN

 

PAHAMILAH VIDEO DI BAWAH INI !

 

Materi ini bisa kalian baca di LKS Matematika Peminatan halaman 15 s/d 16

KERJAKAN : Tugas Individu

DARING 25 AGUSTUS 2021

 MENENTUKAN NILAI LIMIT dengan RUMUS DASAR LIMIT FUNGSI TRIGONOMETRI

 Pahamilah Video di Bawah Ini !

Materi ini bisa kalian baca di LKS Matematika Peminatan halaman 13 dan 14

Tugas Individu : Tugas Individu

DARING 11 AGUSTUS 2021

MENYELESAIKAN LIMIT FUNGSI TRIGONOMETRI DENGAN SUBSTITUSI LANGSUNG

Pahamilah Video di Bawah Ini !

Materi ini bisa kalian pelajari di LKS Matematika Peminatan halaman 12 s/d 13

Kerjakan : TUGAS INDIVIDU 

DARING 4 AGUSTUS 2021

 PENGERTIAN LIMIT FUNGSI MELALUI PENGAMATAN GRAFIK FUNGSI

Pahamilah video di bawah ini !

Materi ini bisa kalian baca di LKS Matematika Wajib halaman 5 s/d 8

Kerjakan : TUGAS INDIVIDU

DARING 28 JULI 2021

 LIMIT FUNGSI ALJABAR

Pahamilah Video di Bawah Ini 

KERJAKAN :TUGAS INDIVIDU

 

DARING KLS 12 MATEMATIKA PEMINATAN ( 17 FEBRUARI 2021 )

 PELUANG BINOMIAL KOMULATIF

PAHAMILAH VIDEO DI BAWAH INI !

KERJAKAN : TUGAS INDIVIDU

DARING KLS 12 MTK PEMINATAN ( 10 FEBUARI 2021 )

 PELUANG BINOMIAL PADA SUATU PERISTIWA

PAHAMILAH VIDEO DI BAWAH INI !

CONTOH SOAL

MATERI INI JUGA BISA DIBACA DI LKS  PEMINATAN HAL 71-75

KERJAKAN : TUGAS INDIVIDU

DARING KLS 12 MTK MINAT ( 27 JANUARI 2021 )

 KONSEP VARIABEL ACAK

PAHAMILAH VIDEO DI BAWAH INI !

KERJAKAN : TUGAS INDIVIDU

DARING KELAS 12 MTK MINAT ( 20 JANUARI 2021 )

 PEMBAHASAN SOAL DISTRIBUSI PELUANG BINOMIAL

Soal

Suatu koin dilempar sebanyak tiga kali. Tentukan peluang mendapatkan tepat dua angka.

Pembahasan 

Permasalahan ini dapat diselesaikan dengan melihat ruang sampelnya. Ruang sampel dari pelemparan satu koin sebanyak tiga kali adalah

S = {AAA, AAG, AGA, GAA, GGA, GAG, AGG, GGG}

Dari ruang sampel, kita dapat melihat bahwa ada tiga cara untuk mendapatkan tepat dua angka, yaitu AAG, AGA, dan GAA. Sehingga peluang kita mendapatkan tepat dua angka adalah 3/8 atau 0,375.

Dengan melihat kembali Contoh 1 dari sudut pandang percobaan binomial, maka contoh tersebut memenuhi keempat kriteria percobaan binomial.

1. Terdapat tiga kali percobaan.
2. Setiap percobaan hanya memiliki dua kemungkinan, yaitu angka (A) atau gambar (G).
3. Hasil dari masing-masing percobaan saling bebas (hasil dari suatu pelemparan tidak mempengaruhi hasil pelemparan lainnya).
4. Peluang percobaan sukses (angka) adalah ½ di setiap percobaannya.

Dalam kasus ini, n = 3, X = 2, p = ½, dan q = ½. Sehingga dengan mensubstitusi nilai-nilai tersebut ke dalam rumus, kita mendapatkan

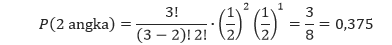
Jawaban tersebut sama dengan jawaban kita sebelumnya yang menggunakan ruang sampel.

Soal

Variabel acak $X$ menyatakan banyak hasil gambar pada pelemparan dua keping mata uang logam. Nilai $P(X=1)$ adalah $\cdots \cdot$

Pembahasan 

Notasi $P(X=1)$ menyatakan peluang munculnya satu gambar pada pelemparan dua keping mata uang logam.
Ruang sampel dari pelemparan dua keping mata uang logam adalah $\left\{\right(A,A),(A,G),(G,A),(G,G\left)\right\}$. Banyak anggota ruang sampelnya ada $4$.
Titik sampel kejadian yang diinginkan adalah $(A,G)$ dan $(G,A)$, ada $2$. Jadi, peluang munculnya satu gambar pada pelemparan dua keping mata uang logam adalah $P(X=1)=\frac{2}{4}=\frac{1}{2}$

$\boxed{{\displaystyle {\displaystyle \frac{\mathrm{<span\; style="color:\; red;">KERJAKAN\; : <a\; href="https://forms.gle/N9ZBSqsH7nSqMQud6">TUGAS\; INDIVIDU</a></span>}}{}}}}$

DARING KELAS 12 MTK MINAT ( 13 JANUARI 2021 )

 

Distribusi Peluang Variabel Acak Diskrit

PAHAMILAH VIDEO DI BAWAH INI !

Materi bisa kalian baca di LKS MATEMATIKA PEMINATAN  halaman 65 s/d 68

KERJAKAN : TUGAS INDIVIDU

KELAS 12 ( DARING 6 JANUARI 2021 )

 

DISTRIBUSI PELUANG BINOMIAL

PAHAMILAH VIDEO DI BAWAH INI !

BI dalam kata BINOMIAL berarti dua. Hal ini merujuk ke setiap kali percobaan atau kesempatan, hasil yang MUNGKIN muncul hanya ada dua.

Pertanyaan yang biasanya muncul adalah, kapan kita menggunakan menghitung peluang dengan menggunakan persamaan distribusi peluang Binomial? Jika kejadian tersebut memenuhi sifat-sifat di bawah ini maka ketika menghitung peluang kejadian tersebut terjadi maka persamaan yang digunakan adalah persamaan peluang dari distribusi binomial.

1. Percobaan dilakukan sebanyak n kali.
2. Setiap kali percobaan mempunyai dua kemungkinan hasil.
3. Kemungkinan hasil dari masing-masing percobaan sama.
4. Hasil yang diperoleh pada percobaan pertama tidak akan mempengaruhi hasil yang diperoleh pada percobaan-percobaan yang lain (saling independen).

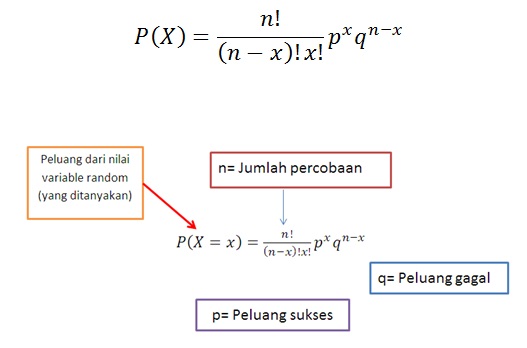
Untuk persamaan hitung peluang dapat dilihat sebagai berikut.

Misalkan X adalah variabel random diskrit. Maka peluang dari X adalah:

Contoh:

Misalkan kita mempunyai satu buah koin yang terdiri atas dua sisi, depan dan belakang. Misalkan kita mengundi sebanyak 10 kali. Pada undian pertama, kemungkinan hasilnya hanya sisi depan atau sisi belakang. Pada undian kedua, kemungkinan hasilnya hanya sisi depan atau sisi belakang. Demikian seterusnya. Setiap kali mengundi, kemungkinan hasilnya sama, hanya dua yaitu sisi depan atau sisi belakang. Dari sepuluh kali percobaan, berapa peluang sisi depan muncul sebanyak dua kali?

Diketahui:

Jumlah percobaan = n = 10.

Peluang sukses = peluang munculnya sisi depan dalam setiap percobaan = p = 0.5.

Peluang gagal = peluang tidak munculnya sisi depan dalam setiap percobaan = q = 1-p = 0.5.

Ditanyakan:

Dari sepuluh kali percobaan, berapa peluang sisi depan muncul sebanyak dua kali? Atau P (X = 2) -> Yang ditanyakan adalah peluang munculnya sisi depan maka kejadian yang dianggap sukses adalah jika sisi depan muncul ketika diundi.

Jawaban:

KERJAKAN : TUGAS INDIVIDU

DARING 4 NOVEMBER 2020

Penentuan Turunan Fungsi Trigonometri dengan Aturan Rantai

Pahamilah Video di Bawah Ini !

KERJAKAN : TUGAS INDIVIDU

DARING 28 OKTOBER 2020

PENENTUAN TURUNAN FUNGSI TRIGONOMETRI BERBENTUK FUNGSI f (u )

Pahamilah Video di Bawah Ini !

Materi bisa kalian baca di lks matematika peminatan kalian hal 38

KERJAKAN : TUGAS INDIVIDU

DARING 21 OKTOBER 2020

 PENENTUAN TURUNAN FUNGSI TRIGONOMETRI DASAR

PAHAMILAH VIDEO DI BAWAH INI !

Berikut ini adalah turunan dari banyak fungsi seperti rumus sin, cos, tan, sec, csc, dan juga tan dalam variabel sudut ax, dimana a merupakan bilangan real dengan a ≠ 0:

• f(x) = sin ax, maka f'(x) = a cos ax
• f(x) = cos ax, maka f'(x) = -a sin ax
• f(x) = tan ax, maka f'(x) = a sec2 ax
• f(x) = sec ax, maka f'(x) = a sec ax. tan ax
• f(x) = csc ax, maka f'(x) = -a csc ax. cot ax
• f(x) = cot ax, maka f'(x) = -a csc2 ax

Materi lebih lengkapnya bisa dibaca di lks matematika minat kalian halaman 34 s/d 37

Kerjakan : TUGAS INDIVIDU

PEMBELAJARAN DARING 30 SEPTEMBER 2020

NILAI LIMIT FUNGSI ALJABAR di TITIK TAK BERHINGGA

PAHAMILAH VIDEO DI BAWAH INI !

Limit Tak Hingga

Untuk menyelesaikan limit tak hingga dari suatu fungsi aljabar, terdapat dua cara yang umum digunakan, yaitu:

Contoh Soal:

Contoh Soal:

Materi ini bisa juga kalian baca di lks matematika peminatan kls 12 hal 21 s/d 23

KERJAKAN : TUGAS INDIVIDU