DARING KLS 8 ( 1 FEBUARI 2021 )

Rumus Perbandingan Sisi-Sisi Pada Segitiga Siku-Siku dengan Sudut Khusus

PAHAMILAH VIDEO DI BAWAH INI !

Rumus Perbandingan Sisi-Sisi Pada Segitiga Siku-Siku dengan Sudut Khusus

Ada dua rumus perbangingan, diantranya :

1. Rumus Perbandingan Sisi-Sisi Pada Segitiga Siku-Siku dengan Sudut 30° dan 60°.
2. Rumus Perbandingan Sisi-Sisi Pada Segitiga Siku-Siku dengan Sudut 45°.

1. Rumus Perbandingan Sisi-Sisi Pada Segitiga Siku-Siku dengan Sudut 30° dan 60°

Berikut rumus perbandingan sisi segitiga dengan sudut 30° dan 60° :

30° : 60° : 90° = 1 : √3  : 2

Untuk bentuk segitiga siku-siku yang bersudut 30° dan 60° bisa dilihat pada gambar di atas.

Contoh soal :

Tentukan AB pada gambar di bawah !

Jawab :

Diketahui :

CB = 10cm

Sudut segitiga siku-siku = 30°, 60°, dan 90°.

Ditanyakan :

AB = ... ???

Karena sudutnya 30°, 60°, dan 90°, maka berlaku :

30° : 60° : 90° = 1 : √3 : 2

Maka :

AC : AB : CB = 1 : √3 : 2

AB : CB = √3 : 2

AB : 10cm = √3 : 2

AB = (10cm x√3 ) : 2

AB = 10√3cm : 2

AB = 5√3cm

Jadi panjang AB adalah 5√3cm.

2. Rumus Perbandingan Sisi-Sisi Pada Segitiga Siku-Siku dengan Sudut 45°

Berikut rumus perbandingan sisi segitiga dengan sudut 45°  :

45° : 45° : 90° = 1 : 1 : √2

Perbandingan panjang sisi-sisi pada segitiga siku-siku sama kaki sebagai berikut.

AB : BC : AC =

Untuk bentuk segitiga siku-siku yang bersudut 45° bisa dilihat pada gambar di atas.

Contoh Soal :

Tentukan AB pada gambar di bawah ini !!

Jawab :

Diketahui :

CB =  10cm

Sudut segitiga siku-siku = 45°, 45°, dan 90°.

Ditanyakan :

AB = ..???

Karena sudutnya 45°, 45°, dan 90°, maka berlaku :

45° : 45° : 90° = 1 : √3 : 2

Maka :

AC :  AB : BC = 1 : 1 : √2

AB : BC = 1 : √2

AB : 10cm = 1 : √2

AB = ( 10cm x 1 ) : √2

AB = 10cm/√2

Untuk lebih menyederhakan kita rasionalkan penyebut dari AB, maka :

AB = ( 10cm/√2  ) x  ( √2 /√2  )

AB = (10cm x √2  ) / ( √2 x√2  )

AB = 10√2cm / 2

AB = 5√2cm

Jadi panjang AB pada gambar di atas adalah 5√2cm

KERJAKAN : TUGAS INDIVIDU

DARING KELAS 10 MTK PEMINATAN ( 27 JANUARI 2021 )

 KESAMAAN DUA VEKTOR PADA BIDANG

PAHAMILAH VIDEO DI BAWAH INI !

KERJAKAN TUGAS : KLIK DI SINI

DARING KLS 12 MTK MINAT ( 27 JANUARI 2021 )

 KONSEP VARIABEL ACAK

PAHAMILAH VIDEO DI BAWAH INI !

KERJAKAN : TUGAS INDIVIDU

DARING KELAS 12 MTK WAJIB ( 26 JANUARI 2021 )

 

Faktorial 

Pahamilah video di bawah ini !

• Dalam matematika, faktorial dari bilangan asli n adalah hasil perkalian antara bilangan bulat positif yang kurang dari atau sama dengan n. 
• Faktorial ditulis sebagai n! dan disebut n faktorial.
•  Bentuk dari faktorial, yaitu:

di mana, untuk 0! = 1! = 1, sehingga:

2! = 2.1 = 2

3! = 3.2.1 = 6

4! = 4.3.2.1 = 24

5! = 5.4.3.2.1 = 120

...dst..

 

Contoh:

Tentukan nilai dari :

CONTOH 

Carilah nilai $x$ pada persamaan di bawah ini.$\frac{x!}{(x-2)!}=6$Jawab:

Cara penyelesaiannya adalah sebagai berikut.$\begin{aligned} \frac{x!}{(x-2)!}&=6\\ \frac{1\times 2\times \cdots\times (x-2)\times (x-1)\times x}{1\times 2\times \cdots\times (x-2)}&=6\\ (x-1)x &=6\\ x^2-x &=6\\ x^2-x-6 &=0 \end{aligned}$Terdapat dua nilai $x$ yang bisa diperoleh dari penyelesaian persamaan di atas, yaitu $x=3$ dan $x=-2.$ Namun demikian, namun demikian faktorial tidak mungkin bernilai negatif, oleh karena itu nilai $x$ yang mungkin adalah $3.$

KERJAKAN : tugas individu

DARING KELAS 10 MTK WAJIB ( 26 JANUARI 2021 )

 UKURAN DERAJAT DAN UKURAN RADIAN

1. Tolong kalian pahami pembahasan soal-soal di bawah ini!.

2. Kalian tulis pembahasan soal ini di buku tulis kalian 

3. Kalian uploud di link : TUGAS

SOAL

Nyatakan besar sudut berikut ke dalam satuan radian!
a. 30° 20′ 15”
b. 106° 20′

Penyelesaian:
a. kita ketahui bahwa:
1” = (1/3600)°
1′ = (1/60)°
1° = 0,0174 radian, maka:
30° 20′ 15”
= 30° + 20.(1/60)° + 15.(1/3600)°
= (108000/3600)° + (1200/3600)° + (15/3600)°
= (109215/3600)°
= (109215/3600).0,0174 radian
= 0,53 rad

b. kita ketahui bahwa:
1′ = (1/60)°
1° = 0,0174 radian, maka:
106° 20′ = 106° + 20.(1/60)°
106° 20′ = (318/3)° + (1/3)°
106° 20′ = (319/3)°
106° 20′ = (319/3).0,0174 radian
106° 20′ = 1,85 rad.

SOAL

Nyatakan sudut 50° ke dalam radian!

Penyelesian:
50° = 50° x π/180°
50° = 0,277π
50° = 0,277 (3,14)
50° = 0,87 radian

SOAL

Nyatakan sudut 0,45 radian  ke dalam satuan derajat!

Penyelesaian:
0,45 radian = 0,45 x 180°/π
0,45 radian = 25,80°

---

DARING KELAS 8 ( 25 JANUARI 2021 )

 PEMBAHASAN SOAL TEOREMA PHYTAGORAS

1. Tolong kalian pahami pembahasan soal-soal di bawah ini!.

2. Kalian tulis pembahasan soal ini di buku tulis kalian 

3. Kalian uploud di link : TUGAS

Soal 

Tentukan jenis segitiga berikut apabila diketahui panjang sisi-sisinya yaitu 10 cm, 12 cm, dan 15 cm!

Jawab:

Misalknya c merupakan sisi terpanjang dan b, a merupakan dua sisi lainnya, maka dapat kita ketahui:

• c = 15 cm
• b = 10 cm
• a = 12 cm.

c² = 15² = 225

a²  + b² = 12²  + 10² = 144 + 100 = 344

Sebab,

c² < a²  + b²
225 < 344

Sehingga, segitiga tersebut termasuk ke dalam segitiga lancip.

Soal 

Diketahui segitiga siku-siku DEF dengan siku-siku di E digambarkan seperti di bawah ini:

Tentukan panjang sisi DE pada gambar di atas!

Jawab:

Sebab segitiga DEF di atas merupakan segitiga siku-siku, maka berlaku rumus Phytagoras seperti di bawah ini:

DF² = DE² + EF²
DE² = DF² – EF²
DE² = 15² – 9²
DE² = 225 – 81
DE² = 144
DE  =  √144
DE = 12

Sehingga, panjang sisi DE pada segitiga siku-siku di atas yaitu 12 cm.

 soal: 

Sebuah persegi ABCD mempunyai panjang 8 cm dan lebar 6 cm. Tentukanlah panjang diagonal dari persegi tersebut.

Jawab: 

Diketahui:

• panjang = p = 8 cm
• lebar = L = 6 cm

Ditanya:

• diagonal = d = … ?

Berdasarkan dalil Pythagoras, maka:

⇒ d2 = p2 + L2
⇒ d2 = 82 + 62
⇒ d2 = 64 + 36
⇒ d2 = 100
⇒ d = √100
⇒ d = 10 cm

Sehingga, panjang diagonal persegi pada soal di atas adalah 10 cm.

DARING KELAS 10 MATEMATIKA PEMINATAN ( 20 JANUARI 2021 )

 PANJANG VEKTOR

      SOAL

SOAL

JAWAB :10

 

KERJAKAN : TUGAS INDIVIDU

DARING KELAS 12 MTK MINAT ( 20 JANUARI 2021 )

 PEMBAHASAN SOAL DISTRIBUSI PELUANG BINOMIAL

Soal

Suatu koin dilempar sebanyak tiga kali. Tentukan peluang mendapatkan tepat dua angka.

Pembahasan 

Permasalahan ini dapat diselesaikan dengan melihat ruang sampelnya. Ruang sampel dari pelemparan satu koin sebanyak tiga kali adalah

S = {AAA, AAG, AGA, GAA, GGA, GAG, AGG, GGG}

Dari ruang sampel, kita dapat melihat bahwa ada tiga cara untuk mendapatkan tepat dua angka, yaitu AAG, AGA, dan GAA. Sehingga peluang kita mendapatkan tepat dua angka adalah 3/8 atau 0,375.

Dengan melihat kembali Contoh 1 dari sudut pandang percobaan binomial, maka contoh tersebut memenuhi keempat kriteria percobaan binomial.

1. Terdapat tiga kali percobaan.
2. Setiap percobaan hanya memiliki dua kemungkinan, yaitu angka (A) atau gambar (G).
3. Hasil dari masing-masing percobaan saling bebas (hasil dari suatu pelemparan tidak mempengaruhi hasil pelemparan lainnya).
4. Peluang percobaan sukses (angka) adalah ½ di setiap percobaannya.

Dalam kasus ini, n = 3, X = 2, p = ½, dan q = ½. Sehingga dengan mensubstitusi nilai-nilai tersebut ke dalam rumus, kita mendapatkan

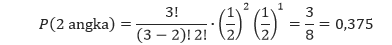
Jawaban tersebut sama dengan jawaban kita sebelumnya yang menggunakan ruang sampel.

Soal

Variabel acak $X$ menyatakan banyak hasil gambar pada pelemparan dua keping mata uang logam. Nilai $P(X=1)$ adalah $\cdots \cdot$

Pembahasan 

Notasi $P(X=1)$ menyatakan peluang munculnya satu gambar pada pelemparan dua keping mata uang logam.
Ruang sampel dari pelemparan dua keping mata uang logam adalah $\left\{\right(A,A),(A,G),(G,A),(G,G\left)\right\}$. Banyak anggota ruang sampelnya ada $4$.
Titik sampel kejadian yang diinginkan adalah $(A,G)$ dan $(G,A)$, ada $2$. Jadi, peluang munculnya satu gambar pada pelemparan dua keping mata uang logam adalah $P(X=1)=\frac{2}{4}=\frac{1}{2}$

$\boxed{{\displaystyle {\displaystyle \frac{\mathrm{<span\; style="color:\; red;">KERJAKAN\; : <a\; href="https://forms.gle/N9ZBSqsH7nSqMQud6">TUGAS\; INDIVIDU</a></span>}}{}}}}$