Senin, 03 Agustus 2020

PEMBELAJARAN DARING 4 AGUSTUS 2020

PEMBAHASAN SOAL

Kedudukan Titik, Garis, dan Bidang pada Bangun Ruang

ASSALAMUALAIKUM WR.WB

Selamat pagi anak2 ku semuanya....selalu semangat untuk belajar di rumah ya....jaga kesehatan dan tetap di rumah saja.Semoga kalian dalam keadaan sehat selalu.Sebelum pembelajaran di mulai terlebih dahulu kalian berdoa.

SOAL

Perhatikan gambar kubus ABCD.EFGH !

contoh soal un jarak bidang ke bidang

Jarak bidang ACH dan EGB adalah ….

Pembahasan:

Perhatikan gambar di bawah!

Jarak bidang ACH dan EGB sama dengan jarak dari titik P ke titik Q. Dari mana rumus umum $PQ = \frac{1}{3}DF$ diperoleh? Lihat ulasan lebih lengkapnya melalui halaman ini.

Mencari panjang BD:

$BD = AB\sqrt{2}$

$BD = 6 \sqrt{3} \cdot \sqrt{2}$

$BD = 6 \sqrt{6}$

Mencari panjang DF:

$DF = \sqrt{BD^{2} + BF^{2}}$

$DF = \sqrt{ \left( 6 \sqrt{6} \right)^{2} + \left( 6 \sqrt{3} \right)^{2}}$

$DF = \sqrt{ 36 \cdot 6 + 36 \cdot 3}$

$DF = \sqrt{ 216 + 108}$

$DF = \sqrt{ 324}$

$DF = 18 \; cm$

Mencari panjang PQ:

$PQ = \frac{1}{3} DF$

$PQ = \frac{1}{3} \cdot 18 = 6 \; cm$

Jadi, jarak bidang ACH dan EGB adalah 6 cm.

SOAL

Perhatikan gambar kubus di bawah!

soal un dimensi tiga

Jarak bidang ACH dan bidang BEG adalah ….

Pembahasan:

Perhatikan gambar di bawah!

soal un dimensi tiga dan pembahasannya

Jarak bidang ACH dan BEG sama dengan jarak dari titik P ke titik Q.

Mencari panjang DF (diagonal ruang):

$DF = sisi \sqrt{3}$

$DF = AB \sqrt{3}$

$DF = 6 \sqrt{3} \; cm$

Mencari panjang PQ:

$PQ = \frac{1}{3} DF$

$PQ = \frac{1}{3} \cdot 6 \sqrt{3} = 2 \sqrt{3} \; cm$

Jadi, jarak bidang ACH dan EGB adalah $2 \sqrt{3}$ cm.

SOAL

Perhatikan gambar kubus ABCD.EFGH!

Contoh soal un dimensi tiga jarak bidang ke bidang

Jarak antara bidang AFH dan bidang BDG adalah ….

Pembahasan:

Perhatikan gambar di bawah!

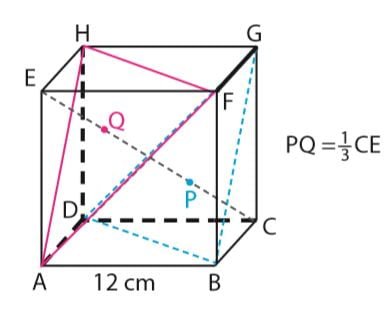
Contoh soal un dimensi tiga jarak bidang ke bidang beserta pembahasannya

Jarak bidang AFH dan bidang BDG sama dengan jarak dari titik P ke titik Q.

Mencari panjang EC (diagonal ruang):

$EC= sisi \sqrt{3}$

$EC = AB \sqrt{3}$

$EC = 12 \sqrt{3} \; cm$

Mencari panjang PQ:

$PQ = \frac{1}{3} EC$

$PQ = \frac{1}{3} \cdot 12 \sqrt{3} = 4 \sqrt{3} \; cm$

Jadi, jarak bidang AFH dan bidang BDG adalah 4 $\sqrt{3}$ cm.

SOAL

Diketahui kubus ABCD.EFGH dengan panjang rusuk 4 cm. Tentukan jarak antara titik F dengan diagonal ruang BH.

Pembahasan

contoh soal dimensi tiga jarak titik terhadap garis

$BF = 4$

$FH = \sqrt{EF^2 + EH^2} = \sqrt{4^2 + 4^2} = 4\sqrt{2}$

$BH = \sqrt{FH^2 + BF^2} = \sqrt{(4\sqrt{2})^2 + 4^2} = 4\sqrt{3}$

Jarak titik F dengan garis BH sama dengan panjang garis PF. Jika luas segitiga BHF diketahui

Luas BHF = $\frac{1}{2}PF \times BH$ atau Luas BHF = $\frac{1}{2}BF \times FH$ , maka:

$\frac{1}{2}PF \times BH = \frac{1}{2}BF \times FH$

$PF \times BH = BF \times FH$

$PF = \frac{BF \times FH}{BH}$

$PF = \frac{4 \times 4\sqrt{2}}{4\sqrt{3}}$

$PF = \frac{4}{3}\sqrt{6 cm}$

BUKTI PENGERJAAN : TUGAS INDIVIDU

Tidak ada komentar:

Posting Komentar

Langganan: Posting Komentar (Atom)