PEMBELAJARAN DARING 27 JULI 2020

ASSALAMUALAIKUM WR.WB

SEBELUM KALIAN PEMBELAJARAN ONLINE HARI INI  TERLEBIH DAHULU KALIAN MEMBACA DOA 

Pengertian Pola Bilangan : Macam Jenis dan Contoh Pola Bilangan Lengkap

Pengertian Pola Bilangan

Definisi pola bilangan matematika adalah susunan dari beberapa angka yang dapat membentuk pola tertentu.

Macam Macam Pola Bilangan

Sebelum kalian membaca materi di bawah ini

Pahami video di bawah ini !

 

Rangkuman materi

Pola Bilangan Ganjil

Pengertian pola bilangan ganjil adalah pola bilangan yang terbentuk dari bilangan-bilangan ganjil.

Pola Bilangan Genap

Pengertian pola bilangan genap adalah pola bilangan yang terbentuk dari bilangan-bilangan genap .

Pola Bilangan Persegi

Pengertian pola bilangan persegi adalah suatu barisan bilangan yang membentuk suatu pola persegi . Pola bilangan persegi adalah 1 , 4 , 9 , 16 , 25 , . . .

Gambar Pola Bilangan Persegi

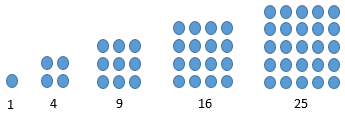Rumus Pola Bilangan Persegi

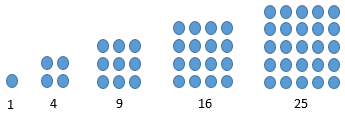
1 , 4 , 9 , 16 , 25 , 36 , . . . , n maka rumus untuk mencari pola bilangan persegi ke-n adalah:

Un = n2

Pola Bilangan Persegi Panjang

Pengertian pola bilangan persegi panjang adalah suatu barisan bilangan yang membentuk pola persegi panjang . Pola persegi panjang adalah 2 , 6 , 12 , 20 , 30 , . . .

Gambar Pola Bilangan Persegi Panjang

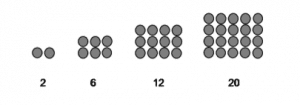
Rumus Pola Bilangan Persegi Panjang

2 , 6 , 12 , 20 , 30 , . . . n , maka rumus pola bilangan persegi panjang ke-n adalah:

Un = n . n + 1

Pola Bilangan Segitiga

Pengertian bola bilangan segitiga adalah suatu barisan bilangan yang membentuk sebuah pola bilangan segitiga. Pola bilangan segitiga adalah 1 , 3 , 6 , 10 , 15 , . . .

Gambar Pola Bilangan Segitiga

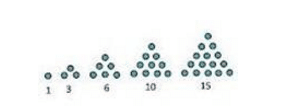
Rumus Pola Bilangan Segitiga

1 , 3 , 6 , 10 , 15 , 21 , 28 , 36 , . . . , ke n . Maka rumus pola bilangan segitiga ke n adalah:

Un = 1/2 n ( n + 1 )

Pola Bilangan Aritmatika

Pengertian pola bilangan aritmatika adalah pola bilangan dimana bilangan sebelum dan sesudahnya memiliki selisih yang sama. Contoh pola bilangan aritmatika adalah 2, 5, 8, 11, 14, 17, ….

Suku pertama dalam bilangan aritmatika disebut dengan awal ( a ) atau U1, sedangkan suku kedua adalah U2 dan seterusnya.

Selisih dalam barisan aritmatika disebut dengan beda dan dilambangkan dengan b.
Karena bilangan sebelum dan sesudahnya memiliki selisih yang sama, maka b = U2 – U1 

Rumus mencari suku ke-n adalah Un = a + (n -1) b

klik disini : tugas individu