DARING KELAS 8 ( 18 JANUARI 2021 )

 
Menentukan diagonal ruang kubus dan juga balok

PAHAMILAH VIDEO DI BAWAH INI !

Diberikan suatu balok ABCD.EFGH seperti yang terlihat pada gambar di bawah ini:

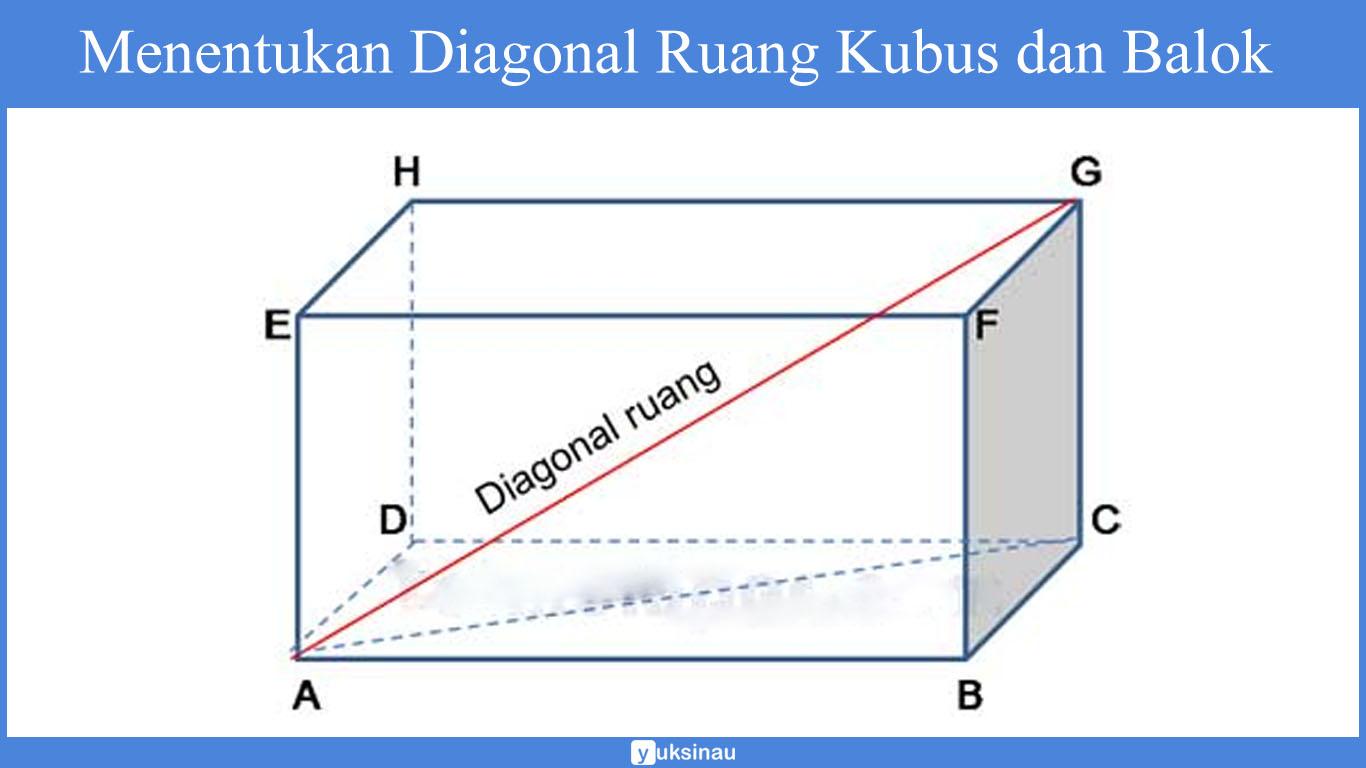
Garis AG merupakan salah satu diagonal ruang dalam balok tersebut. Panjang diagonal ruang AG bisa kita hitung berdasarkan dalil Pythagoras seperti berikut ini:

AG2 = AC2 + CG2

Keterangan: 

AG = diagonal ruang
CG = tinggi balok
AC = diagonal bidang alas

Kemudian perhatikan alas balok yakni persegi ABCD. Berdasarkan dari bunyi Pythagoras, panjang diagonal bidang AC bisa kita hitung dengan menggunakan rumus berikut:

AC2 = AB2 + BC2

Keterangan:

AB = panjang balok
BC = lebar balok

Sebab, AC2 = AB2 + BC2, maka rumus panjang diagonal ruang AG bisa kita ubah menjadi:

⇒ AG2 = AC2 + CG2
⇒ AG2 = AB2 + BC2 + CG2
⇒ AG2 = p2 + L2 + t2

Sehingga, rumusnya akan menjadi:

dr2 = p2 + L2 + t2

Keterangan:

dr = diagonal ruang
p = panjang balok
L = lebar balok
t = tinggi balok

Contoh soal: 

Suatu balok memiliki panjang, lebar, dan tinggi berturut-turut yaitu 12 cm, 9 cm, dan 8 cm. Tentukanlah panjang salah satu diagonal ruangnya!

Jawab: 

Diketahui:

• p = 12 cm
• L = 9 cm
• t = 8cm

Ditanya:

• dr = … ?

Berdasarkan dari bunyi atau dalil Pythagoras, maka:

⇒ dr2 = p2 + L2 + t2
⇒ dr2 = 122 + 9sup>2 + 82
⇒ dr2 = 144 + 81 + 64
⇒ dr2 = 289
⇒ dr = √289
⇒ dr = 17 cm

Sehingga, panjang diagonal ruangnya yaitu 17 cm.

KERJAKAN  :TUGAS INDIVIDU