DARING 16 NOVEMBER 2020

 PERSAMAAN GARIS LURUS 

Pahamilah Video di bawah ini !

Persamaan garis lurus adalah persamaan yang membentuk garis lurus saat digambarkan dalam bidang kartesius. 

Bentuknya akan memiliki dua variabel yang masing-masing variabelnya punya pangkat (orde) tertinggi satu. Contohnya, 2x + y = 4, 3y = x - 6, x + y - 2 = 0, dan masih banyak lagi.

Terdapat tiga langkah dalam membuat grafik dari persamaan garis lurus. Supaya kamu lebih mudah memahami, kita langsung masuk ke contoh soalnya aja ya.

Contoh Soal:

Gambarlah grafik dari persamaan garis lurus y = 3x - 9!

1. Cari titik potong di sumbu x

Cara mencari titik potong pada sumbu x adalah dengan membuat variabel y menjadi 0.

Jadi, saat y = 0, nilai x yang dihasilkan adalah 2. Sehingga, diperoleh titik potong di sumbu x adalah (3,0).

2. Cari titik potong di sumbu y

Tidak jauh berbeda dengan cara mencari titik potong pada sumbu x, untuk mencari titik potong di sumbu y, kita harus mengganti variabel x menjadi 0.

Jadi, saat x = 0, nilai y yang dihasilkan adalah -6. Sehingga, diperoleh titik potong di sumbu y adalah (0,-9).

3. Gambar garis yang menghubungkan titik potong tersebut

Setelah diperoleh dua buah titik potongnya, kita bisa tarik garis lurus yang menghubungkan kedua titik potong tersebut. Sehingga, hasilnya akan seperti ini.

KERJAKAN : TUGAS INDIVIDU

DARING 9 NOVEMBER 2020

 FUNGSI / PEMETAAN

PAHAMILAH VIDEO DI BAWAH INI !

Contoh

Jika diketahui fungsi g(x) = ax + b dengan g(2) = 4 dan g(-3) = -11, tentukan
a. Nilai a dan b
b. Rumus fungsi g
c. Peta dari 3
Jawab
a. g(x) = ax + b
g(2) = 4 maka 2a + b = 4
g(-3) = -11 maka -3a + b = -11
Eliminasi b
2a + b = 4
-3a + b = -11  -
5a = 15
a = 3
Substitusi a = 3 ke 2a + b = 4
6 + b = 4
b = 4 - 6
b = -2
Jadi, nilai a = 3 dan b = -2
b. g(x) = 3x - 2
c. g(x) = 3x -2
g(3) = 3(3) - 2 = 7
Jadi, peta dari 3 adalah 7

Menentukan Banyaknya Fungsi yang Dapat Dibuat dari Dua Himpunan

Untuk menentukkan banyaknya suatu fungsi yang mungkin dapat dibuat dari dua himpunan kita dapat menggunakan sebuah rumus. Misalkan himpunan A dan himpunan B dengan jumlah anggota A adalah n(A) dan jumlah anggota himpunan B adalah n(B), banyaknya fungsi atau pemetaan dari himpunan A ke himpunan B yang dapat dibuat adalah

A ke B = n(B)n(A)${}^{n(A)}$

Sedangkan, banyaknya pemetaan dari himpunan B ke himpunan A yang dapat dibuat adalah

B ke A = n(A)n(B)${}^{n(B)}$

Contoh 

Diketahui himpunan A = {himpunan pembentuk kata CERIA} dan himpunan B = {bilangan prima kurang dari 10}. Tentukan banyaknya

a. Pemetaan dari himpunan A ke B

b. Pemetaan dari himpunan B ke A
Jawab
A ={ C, E, R, I, A}
n(A) = 5
B = {2, 3, 5, 7}
n(B) = 4
a. A ke B = n(B)n(A)${}^{n(A)}$ = 45${}^5$ = 1024
b. B ke A = n(A)n(B)${}^{n(B)}$ = 54${}^4$ = 625

KORESPONDENSI SATU - SATU

Korespondensi satu-satu merupakan relasi khusus yang memasangkan setiap anggota himpunan A dengan tepat satu anggota himpunan B dan begitupun sebaliknya. Dengan demikian, banyaknya anggota himpunan A dan himpunan B haruslah sama.

Jika melihat dari syarat korespondensi satu-satu bahwa banyak anggota domain dan kodomain harus sama maka bisa dirumuskan sebagai berikut : Jika n (A) = n(B) = n, maka banyaknya korespondensi satu-satu yang mungkin adalah : n x (n – 1) x (n – 2) x … x 2 x 1.

Contoh Soal 1 :

Diketahui himpunan A = {2, 4, 6, 8, 10, 12} dan himpunan B = {1, 3, 5, 7, 9, 11}. Maka tentukanlah berapa banyak kemungkinan korespondensi satu satu yang dapat dibentuk dari himpunan A ke himpunan B ?

Penyelesaian Soal :

Banyak anggota himpunan A dan Himpunan B adalah sama, yaitu 6 maka n = 6. Oleh karena itu, banyak kemungkinan korespondensi satu satu yang dapat dibentuk adalah sebagai berikut :

6 x 5 x 4 x 3 x 2x 1 = 720

Maka bisa disimpulkan bahwa terdapat 720 korespondensi satu satu yang dapat dibentuk dari himpunan A ke himpunan B.

Contoh Soal 2 :

Berapakan banyaknya jumlah korespondensi satu-satu yang dapat dibentuk dari himpunan C = (huruf vokal) dan juga D = (bilangan prima yang jumlahnya kurang dari 13) ?

Penyelesaian Soal :

Diketahui :       C = Huruf Vokal = a, i, u, e, o

D = Bilangan Prima yang Kurang dari 13 = 2, 3, 5, 7, 11

Karena n (C) dan n (D) = 5 maka untuk jumlah korespondensi satu-satu antara himpunan C dengan D adalah sebagai berikut : 5? = 5 x 4 x 3 x 2 x 1 = 120

Maka dapat disimpulkan bahwa jumlah korespondensi satu-satu dari himpunan C (huruf vokal) dan juga D (bilangan prima yang jumlahnya kurang dari 13) adalah 120.

KERJAKAN : TUGAS INDIVIDU

DARING 3 NOVEMBER 2020

   Menyajikan Data dalam Bentuk Diagram 

(Statistika Data Tunggal )

1. Diagram Garis

Penyajian data statistik dengan memakai diagram berbentuk garis lurus disebut dengan diagram garis lurus atau diagram garis.

Diagram garis pada umumnya dimanfaatkan guna menyajikan data statistik yang didapatkan berdasarkan pengamatan dari masa ke masa secara berurutan.

Sebagai contoh: simulasi diagram garis yang biasa kalian ubah dari diagram garis yang ada.

Contoh Soal

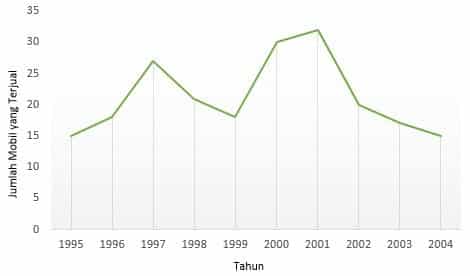
Pada akhir 1995 – 2004, dealer mobil selalu mencatat jumlah mobil yang dijual, berikut adalah laporannya :

Maka, pembuatan diagram garis pada contoh soal di atas adalah :

Diagram di atas menunjukkan bahwa sebagian besar penjualan mobil terjadi pada tahun 2001. Penjualan mobil cenderung meningkat antara 1995 hingga tahun 1997, sedangkan cenderung menurun antara tahun 2002 hingga tahun 2004.

2. Diagram Batang

Diagram batang pada umumnya dipakai untuk menggambarkan perkembangan nilai dari sebuag objek penelitian dalam kurun waktu tertentu.

Diagram batang menggambarkan berbagai keterangan dengan berabgai gambar batang tegak atau mendatar dan sama lebar dengan batang-batang terpisah.

Contoh Soal

perhatikan tabel yang menyajikan data suhu terendah dan tertinggi dari beberapa kota berikut!

Dari tabel tersebut kita dapat menggambar diagram batang yang menyajikan suhu terendah dan tertinggi dari masing-masing kota sekaligus. Perhatikan diagram batang berikut!

Dari diagram batang ini kita dapat membandingkan suhu terendah dan suhu tertinggi sekaligus dari masing-masing kota.

3. Diagram Lingkaran

Diagram lingkaran merupakan penyajian data statistik dengan memakai gambar yang berbentuk lingkaran.

Setiap bagian yang berasal dari daerah lingkaran akan menunjukkan bagian-bagian atau persen dari keseluruhan data.

Untuk membuat diagram lingkaran, maka langkah yang harus kalian terlebih dahulu adalah menentukan besarnya persentase pada masing-masing objek terhadap keseluruhan data.

Serta besarnya sudut pusat sektor lingkaran

Rumus :

Nilai yang diperlukan = (nilai sudut/360 °) x nilai total

Contoh Soal :

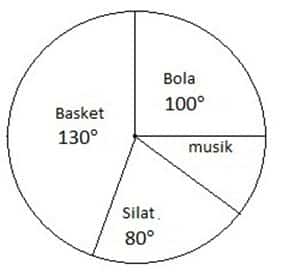
Sebuah sekolah memiliki 1.260 siswa. Di sekolah ini, siswa harus menghadiri kegiatan ekstrakurikuler. Ketika siswa mengambil program ekstrakurikuler dibentuk menjadi diagram lingkaran dalam bentuk derajat (°) sebagai berikut :

Berapa banyak siswa yang mengikuti ekskul musik?

Jawab :

Diketahui :
Total siswa = 1260 siswa
Ekskul basket = 130°
Ekskul bola = 100°
Ekskul silat = 80°

Ditanya :
Banyak siswa yang memilih ekskul musik ekstrakurikuler?

Dijawab :
Pertama, cari tahu berapa banyak siswa yang melakukan musik ekstrakurikuler.
Ekskul musik = 360 ° – (Ekskul basket + ekskul bola + ekskul silat)
= 360° – (130° – 100° – 80°)
= 360° – 310°
= 50°

Kemudian gunakan rumus untuk menentukan jumlah siswa yang belajar musik :
Jumlah siswa yang memilih musik = (musik/360°) x jumlah total siswa
= (50°/360°) x 1260 siswa
= 63000/360
= 175 siswa
Jadi ada 175 siswa yang melakukan musik ekstrakurikuler

Rumus :

Nilai yang ditanyakan = (nilai persentase/100%) x nilai total

Contoh Soal :

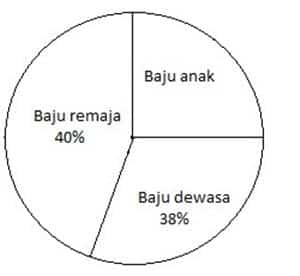
Diketahui dari data di atas, bahwa total barang dagangan yang dijual oleh pedagang adalah 300. Mencari berapa banyak item pakaian untuk anak – anak yang dijual oleh penjual pakaian?

Jawab :

Diketahui :
Total pakaian = 300 bagian
Pakaian remaja = 40%
Pakaian dewasa = 38%

Ditanya :
Berapa banyak baju anak yang dijual?

Dijawab :
Pertama, lihat persentase pakaian anak – anak yang dijual.
Persentase pakaian anak = 100% – (pakaian remaja + pakaian dewasa)
= 100% – (40% + 38%)
= 100% – 78%
= 22%

Jadi gunakan persentase pakaian anak yang Anda dapatkan dalam rumus diatas.
Jumlah pakaian anak = (persentase anak / 100%) x pakaian keseluruhan
= (22% / 100%) × 300 buah
= 6600/100
= 66 buah
Jumlah pakaian anak – anak yang dijual oleh pedagang adalah 66 buah.

KERJAKAN : TUGAS INDIVIDU